MODELO DE EXAMEN 1996-97
|
| MATERIA: Dibujo Técnico |
TIEMPO: 90 minutos |
INSTRUCCIONES:
- A continuación se presentan dos repertorios de cuestiones, el A) y el B).
Cada alumno deber elegir, a voluntad, uno de los dos repertorios completos para realizar
la prueba.
La respuesta, que será fundamentalmente gráfica, se hará a lápiz y con la
instrumentación adecuada, dejando indicadas las construcciones auxiliares para que pueda
seguirse el proceso resolutivo, si ello fuera necesario.
Si el alumno añadiese comentarios escritos, se harán en forma concisa con pluma o
bolígrafo.
|
| REPERTORIO A |
| 1A) |
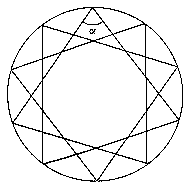
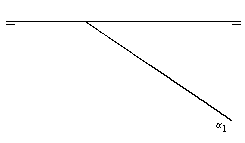
Deducir razonadamente el valor del ángulo a
marcado en la figura, sabiendo que ésta representa un decágono regular estrellado. (2
puntos) |
 |
| 2A) |
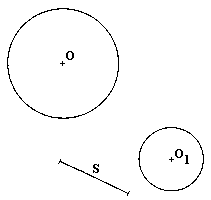
Dibujar los posibles segmentos iguales y paralelos al segmento s,
de modo que sus extremos estén en las circunferencias de centros O y O1.
(2 puntos) . |
 |
| 3A) |
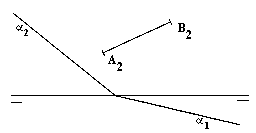
Hallar la verdadera magnitud del segmento AB que pertenece al plano a y del que se conoce la proyección vertical A2
B2.(2 puntos) |
 |
| 4A) |
Hallar las trazas del plano que pasa por el punto P y que es paralelo
a las generatrices del cono que pasan por los puntos Q y R pertenecientes
a la superficie cónica y de los que se conocen sus proyecciones horizontales. (2 puntos).
|
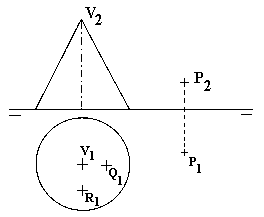 |
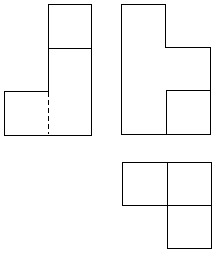
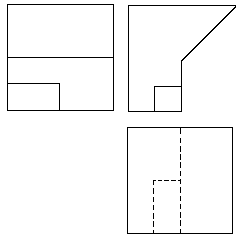
| 5A) |
Dada la planta, alzado y perfil del sólido de la figura, dibujar una perspectiva
isométrica del mismo a la misma escala y sin tener en cuenta coeficientes de reducción.
(2 puntos). |
 |
|
| REPERTORIO B |
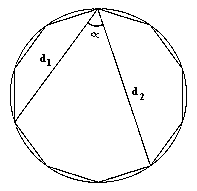
| 1B) |
Deducir razonadamente el ángulo a que
forman las diagonales d1 y d2 de un decágono
regular. (2 puntos). |
 |
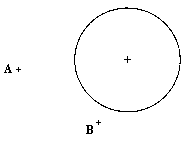
| 2B) |
Dibujar las circunferencias tangentes a la circunferencia dada y que pasen por los
puntos A y B. (2 puntos). |
 |
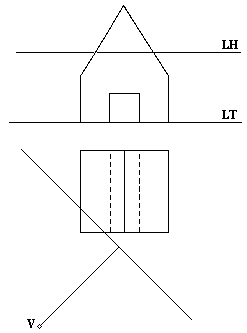
| 3B) |
Dibujar la perspectiva cónica del cuerpo dado en diédrica y cuya situación del
plano del cuadro y punto de vista vienen dadas en el esquema adjunto. (2 puntos) |
 |
| 4B) |
El triángulo ABC está contenido en el plano a
y de él se conoce la proyección horizontal. Hallar la proyección vertical. |
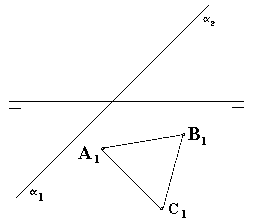 |
| 5B) |
Dibujar en su plano y en verdadera magnitud la sección principal de un cubo de 4
cm. de arista. (2 puntos). |
|
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE SEPTIEMBRE DE 1.997
|
| MATERIA: Dibujo Técnico |
TIEMPO: 90 minutos |
INSTRUCCIONES:
- A continuación se presentan dos repertorios de cuestiones, el A) y el B).
Cada alumno deber elegir, a voluntad, uno de los dos repertorios completos para realizar
la prueba.
La respuesta, que será fundamentalmente gráfica, se hará a lápiz y con la
instrumentación adecuada, dejando indicadas las construcciones auxiliares para que pueda
seguirse el proceso resolutivo, si ello fuera necesario.
Si el alumno añadiese comentarios escritos, se harán en forma concisa con pluma o
bolígrafo.
|
| REPERTORIO A |
| 1A) |
Hallar la figura transformada de la dada después de
aplicarle un giro de 45º en sentido horario alrededor del punto A y una homotecia de
razón k = 5/3 de centro en el mismo punto. (2 puntos) |
 |
| 2A) |
Dadas las tres rectas paralelas r, s y t,
construir un cuadrado teniendo en cuenta que tres de sus vértices han de quedar
contenidos en las citadas rectas. (2 puntos). 
|
| 3A) |
Dada la recta de perfil definida por sus trazas H y V, trazar por el
punto A los planos paralelos a ella y que formen 45º con el horizontal de la proyección.
(2 puntos). |
 |
| 4A) |
Hallar las trazas de un plano que contenga a los puntos A, B y C. (2
puntos). |
 |
| 5A) |
Dibujar una perspectiva isométrica de la figura dada por sus
proyecciones. No hay que tener en cuenta los coeficientes de reducción de los ejes. (2
puntos) |
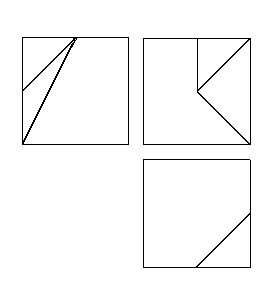 |
|
| REPERTORIO B |
| 1B) |
Contruir un triángulo semejante al ABC y que tenga de perímetro 180
mm. (2 puntos) |
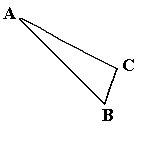 |
| 2B) |
Definida una elipse por sus focos F, F’ y un punto A de la misma,
dibujar sus ejes y la targente en el punto A. No borrar las construcciones auxiliares. (2
puntos) |
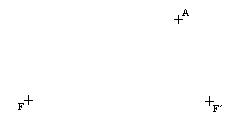 |
| 3B) |
Dibujar las proyecciones diédricas de un triángulo equilátero ABC
contenido en el plano a . Se
conoce la proyección horizontal del vértice A y la vertical del vértice B. Se sabe
además que el triángulo queda totalmente contenido en el primer cuadrante. (2 puntos) |
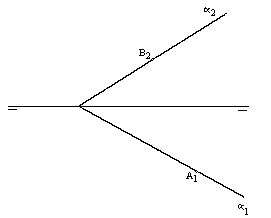 |
| 4B) |
Se conoce la traza horizontal a 1 de un plano que forma 60º con el plano horizontal. Dibujar la
traza vertical de dicho plano a
. ¿Cuántas soluciones hay? (2 puntos) |
 |
| 5B) |
Dibujar una perspectiva isométrica del sólido dado sin tener en
cuenta el coeficiente de reducción.(2 puntos) |
 |
|
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE JUNIO DE 1.997
|
| MATERIA: Dibujo Técnico |
TIEMPO: 90 minutos |
INSTRUCCIONES:
- A continuación se presentan dos repertorios de cuestiones, el A) y el B).
Cada alumno deber elegir, a voluntad, uno de los dos repertorios completos para realizar
la prueba.
La respuesta, que será fundamentalmente gráfica, se hará a lápiz y con la
instrumentación adecuada, dejando indicadas las construcciones auxiliares para que pueda
seguirse el proceso resolutivo, si ello fuera necesario.
Si el alumno añadiese comentarios escritos, se harán en forma concisa con pluma o
bolígrafo.
|
| REPERTORIO A |
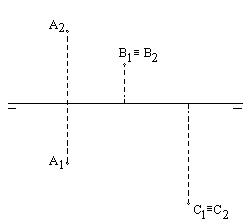
| 1A) |
Dadas las circunferencias C1 y C2,
hallar los puntos P del plano desde los que se pueden trazar tangentes a
ambas circunferencias, tales que la distancia del punto P al punto de
contacto sea 35 mm. (2 puntos) |
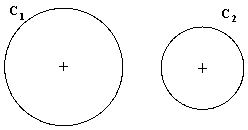 |
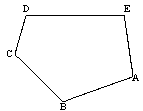
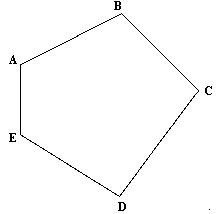
| 2A) |
Dibujar la figura homotética de la ABCDE con centro O
y razón de homotecia 1/2. (2 puntos). |
 |
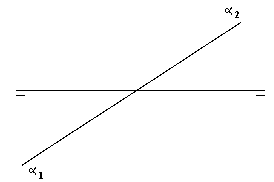
| 3A) |
Un cubo se apoya en el plano horizontal de proyección sobre una arista
AB del mismo, teniendo además paralela a dicho plano una de sus secciones principales.
Conociendo la proyección horizontal A1B1 de la arista de apoyo,
completar las proyecciones del cubo. (2 puntos) |
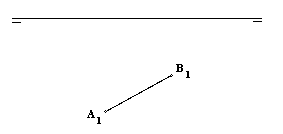 |
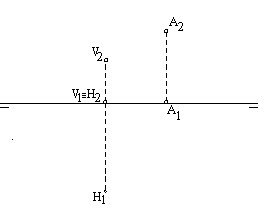
| 4A) |
Hallar la proyección horizontal del cuadrilátero ABCD,
sabiendo que está contenido en el plano a . (2 puntos) |
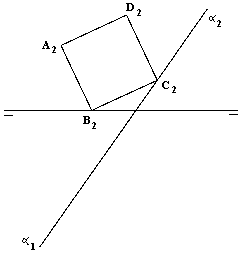 |
| 5A) |
Dibujar una perspectiva isométrica del sólido dado sin tener en
cuenta el coeficiente de reducción. (2 puntos) |
 |
|
| REPERTORIO B |
| 1B) |
Dibujar un triángulo rectángulo cuya hipotenusa mida 80 mm.
y la altura sobre ella sea de 35 mm. No borrar las construcciones
auxiliares. (2 puntos) |
| 2B) |
Hallar gráficamente el perímetro de un triángulo A’B’C’
cuyo lado mayor mide 50 mm., sabiendo además que es semejante a otro
triángulo ABC cuyos lados miden a = 35 mm., b = 30 mm.
y c = 25 mm. (2 puntos) |
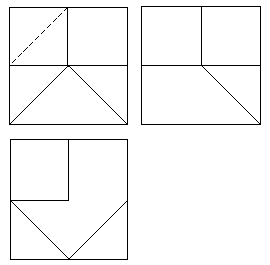
| 3B) |
Hallar los ángulos que forma el plano a con el horizontal y el vertical de
proyección. (2 puntos) |
 |
| 4B) |
Hallar la recta de intersección del plano a con el definido por la línea de
tierra y el punto A. (2 puntos) |
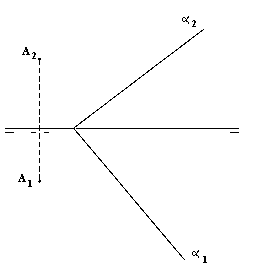 |
| 5B) |
Dibujar una perspectiva isométrica del sólido dado sin tener en
cuenta el coeficiente de reducción. (2 puntos) |
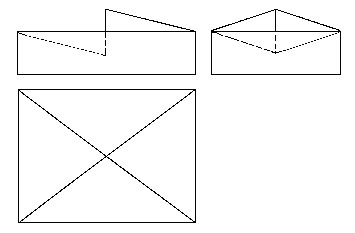 |
|
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE JUNIO DE 1.996
|
| MATERIA: Dibujo Técnico |
TIEMPO: 90 minutos |
INSTRUCCIONES:
- A continuación se presentan dos repertorios de cuestiones, el A) y el B).
Cada alumno deber elegir, a voluntad, uno de los dos repertorios completos para realizar
la prueba.
La respuesta, que será fundamentalmente gráfica, se hará a lápiz y con la
instrumentación adecuada, dejando indicadas las construcciones auxiliares para que pueda
seguirse el proceso resolutivo, si ello fuera necesario.
Si el alumno añadiese comentarios escritos, se harán en forma concisa con pluma o
bolígrafo.
|
| REPERTORIO A |
| 1A) |
Dadas las circunferencias C y C’ de la figura,
construir los posibles centros de homotecia que transforman C en C’
e indicar las correspondientes razones de homotecia. (2 puntos) |
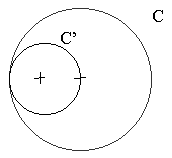 |
| 2A) |
Dado el cuadro ABCD, dibujar un octógono regular en el cual los
vértices del cuadrado sean también vértices del octógono. (2 puntos) |
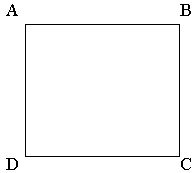 |
| 3A) |
Dada la esfera cuyas proyecciones se indican en la figura, dibujar las proyecciones de
un cubo inscrito en ella de modo que cuatro de sus aristas sean verticales, otras cuatro
de punta y otras cuatro paralelas a la línea de tierra. (2 puntos) |
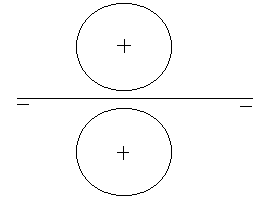 |
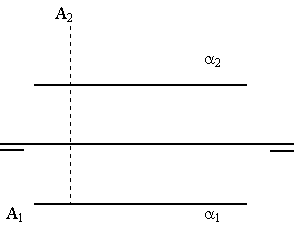
| 4A) |
Hallar la distancia del punto A al plano a.
(2 puntos) |
 |
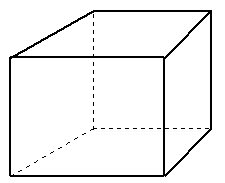
| 5A) |
Dibujar sobre el cubo dado el poliedro resultante de unir los puntos medios de sus
aristas. Interpretar correctamente las partes vistas y ocultas del sólido resultante.
Indicar qué polígonos forman sus caras, el número de aristas y el número de vértices.
(2 puntos) |
 |
|
| REPERTORIO B |
| 1B) |
Dados los puntos A y B y la recta r,
hallar en esta recta un punto P tal que la suma PA + PB
tengan un valor mínimo. (2 puntos) |
 |
| 2B) |
Construir un triángulo rectángulo en el que la hipotenusa valga 8 cm.
y la suma de los catetos sea 10 cm. (2 puntos). |
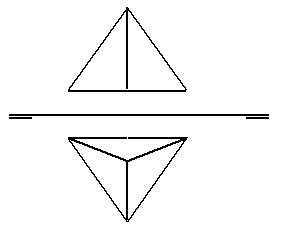
| 3B) |
Hallar las proyecciones de la esfera circunscrita al tetraedro regular de la figura. (2
puntos) |
 |
| 4B) |
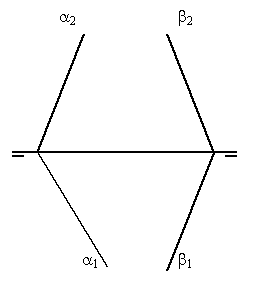
Hallar las proyecciones de la recta de intersección de los planos a
y b cuyas trazas se cortan fuera de los
límites del dibujo. (2 puntos) |
 |
| 5B) |
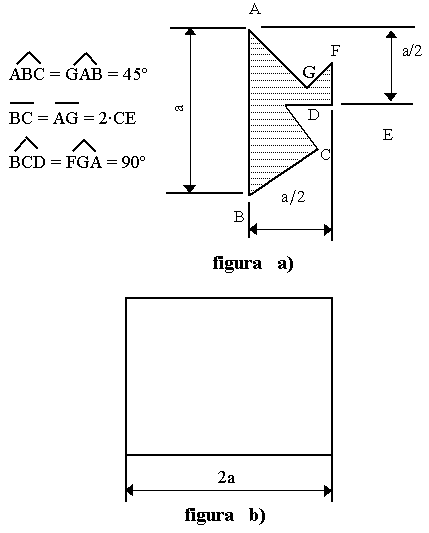
Tenemos unas baldosas cuyas dimensiones principales están dadas en la figura a).
Queremos maciar con ellas el cuadrado de la figura b). Dibujar sobre
dicho cuadrado el resultado de la operación anterior. (2 puntos) |
 |
|
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE SEPTIEMBRE DE 1.996
|
| MATERIA: Dibujo Técnico |
TIEMPO: 90 minutos |
INSTRUCCIONES:
- A continuación se presentan dos repertorios de cuestiones, el A) y el B).
Cada alumno deber elegir, a voluntad, uno de los dos repertorios completos para realizar
la prueba.
La respuesta, que será fundamentalmente gráfica, se hará a lápiz y con la
instrumentación adecuada, dejando indicadas las construcciones auxiliares para que pueda
seguirse el proceso resolutivo, si ello fuera necesario.
Si el alumno añadiese comentarios escritos, se harán en forma concisa con pluma o
bolígrafo.
|
| REPERTORIO A |
| 1A) |
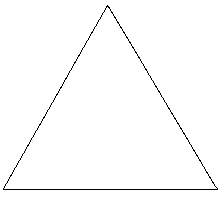
Dado el triángulo equilátero de la figura, trazar en su interior tres
circunferencias de igual radio, siendo cada circunferencia tangente exteriormente a las
otras dos y siendo tangentes, además, a dos lados del triángulo. No borrar las
construcciones auxiliares. (2 puntos) |
 |
| 2A) |
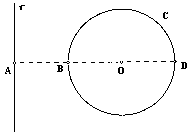
Dada la circunferencia C y la recta r de la figura, en la que se verifica que: AB
= BO = OD = a, indicar cuáles son los posibles centros de inversión que transforman C
en r y cuáles serían las correspondientes potencias de inversión. (2 puntos). |
 |
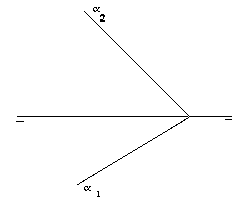
| 3A) |
Hallar el ángulo que forma el plano a con la línea
de la tierra. (2 puntos). |
 |
| 4A) |
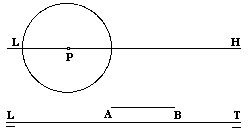
Tenemos una perspectiva lineal dada por su línea de tierra, línea de horizonte,
punto principal y círculo de distancia. Se sabe que AB es la perspectiva de una
arista de la base de un tetraedro regular apoyado sobre el geometral. Si el tercer
vértice C de la base está más alejado de la línea de tierra, completar la
perspectiva del tetraedro interpretando debidamente sus partes vistas y ocultas. Se
recuerda que el radio del círculo de distancia es igual a la distancia que separa el
punto de vista del plano del cuadro. (2 puntos). |
 |
| 5A) |
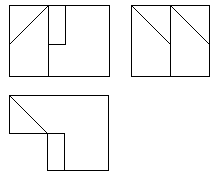
Dada la planta, alzado y perfil del sólido de la figura, dibujar una perspectiva
isométrica del mismo a la misma escala y sin tener en cuenta coeficientes de reducción.
(2 puntos). |
 |
|
| REPERTORIO B |
| 1B |
Construir dos segmentos rectilíneos a y b cuya suma sea 70
mm. y cuya razón sea 5/3. No borrar las construcciones auxiliares. (2 puntos). |
| 2B |
Construir un triángulo rectángulo de perímetro 8 cm. y sabiendo que uno de
sus ángulos agudos mide 60º. No borrar las construcciones auxiliares. (2 puntos).
|
| 3B |
Dibujar las proyecciones de la perpendicular común a las rectas de perfil r
y s en las que se han definido sus trazas. (2 puntos). |
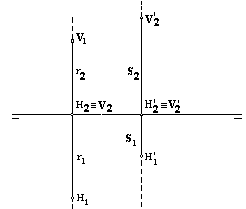 |
| 4B |
Dibujar la proyección vertical del segmento AB, sabiendo que su verdadera
magnitud es de 4 cm. y que el extremo B está más alto que el punto A.
(2 puntos). |
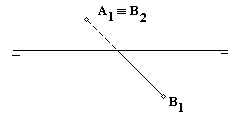 |
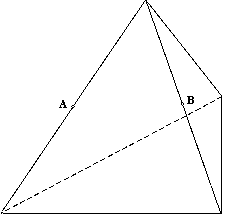
| 5B |
Dado el tetraedro regular de la figura, dibujar sobre él la intersección con un
plano que pasa por los puntos medios A y B de dos aristas y que lo corta a lo largo
de un cuadrado perfecto. (2 puntos). |
 |
|

