Resolución de problemas de tangencias por dilatación

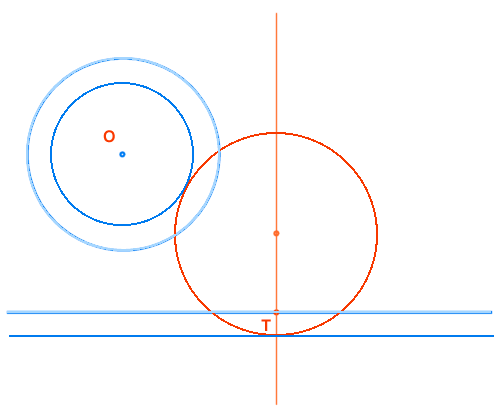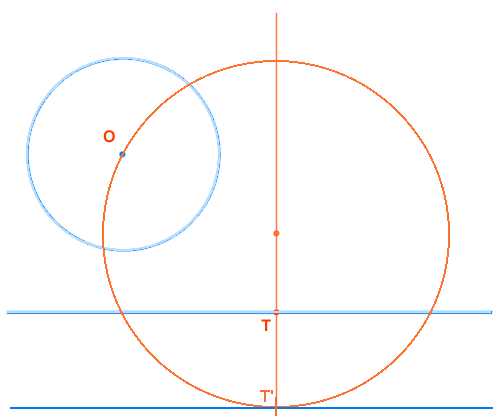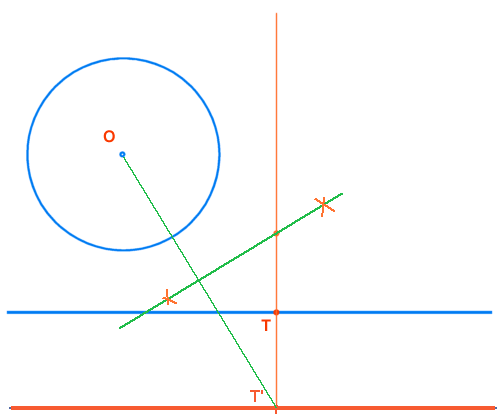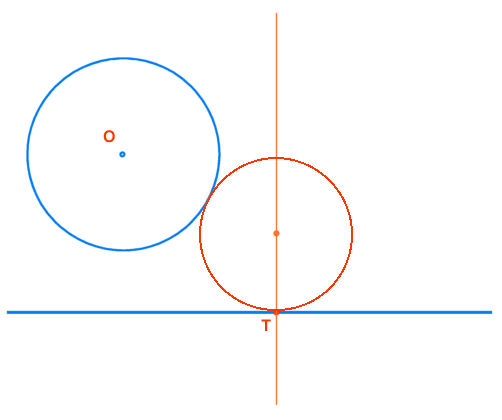
	PROBLEMAS DE TANGENCIAS Se dilata negativamente la circunferencia dada hasta convertirla en un punto (O) y la recta se desplaza una distancia igual al radio de la circunferencia dada La circunferencia tangente a la recta desplazada y que pase por el centro O de la dada TENDRA EL MISMO CENTRO QUE LA SOLUCION (Os)		Resolución de problemas de tangencias por dilatación. En este ejercicio cuyo enunciado es: Hallar la circunferencia Os, tangente a la dada (O) y a la recta, conociendo el punto de tangencia en la recta (T).


			Resolución de problemas de tangencias por INVERSIÓN. En este ejercicio cuyo enunciado es: Hallar la circunferencia Os, tangente a la dada (O) y a la recta, conociendo el punto de tangencia en la recta (T)
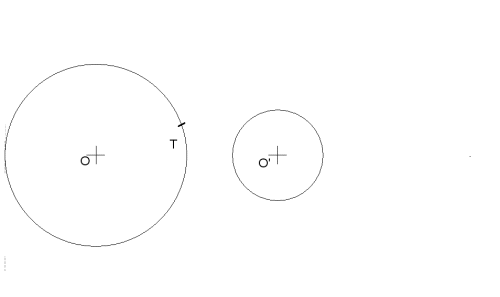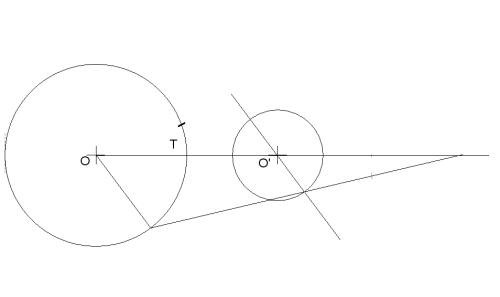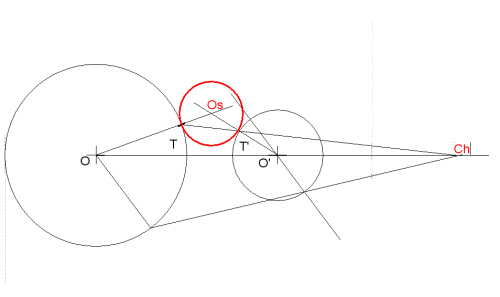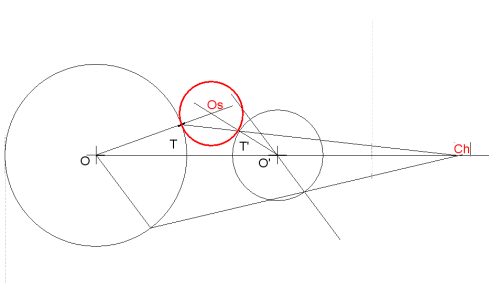
	la circunferencia(O) y la recta se convierten en figuras inversas eligiendo el Centro de Inversión en el extremo del diámetro perpendicualar a la recta.
	Al unirlo con el punto T se obtiene el INVERSO T' en la circunferencia. Aplicando los teoremas de las tangencias se obtiene Os (centro de la solución)

			Resolución de problemas de tangencias por INVERSIÓN. En este ejercicio cuyo enunciado es: Hallar la circunferencia Os, tangente a las dadas (O y O '), conociendo el punto de tangencia en una de ellas (T)
	La circunferencias(O y O ') se convierten en figuras inversas eligiendo como Centro de Inversión el centro de HOMOTECIA. Al unirlo con el punto T se obtiene el INVERSO T' en la otra circunferencia.

PROBLEMAS DE TANGENCIAS