Resolución de problemas de tangencias por dilatación

Cónicas	Curvas Cónicas (Definición y ejemplos)	Volver a Dibujo Técnico
		Definición geométrica de las cónicas (tangencias)
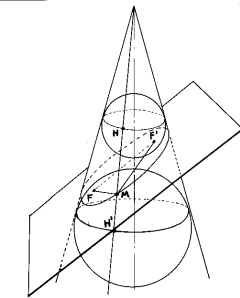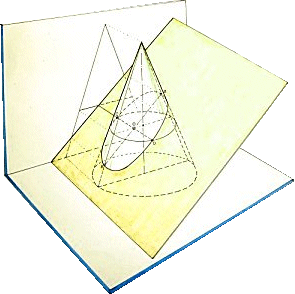
	Definición de elipse: lugar geométrico de puntos que son centros de circunferencias que pasan por el foco y son tangentes a la otra focal.	pulsa para ver en 3D
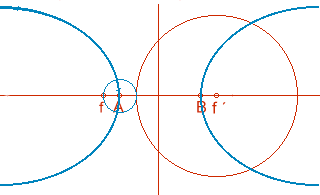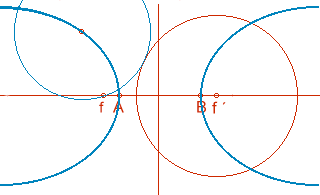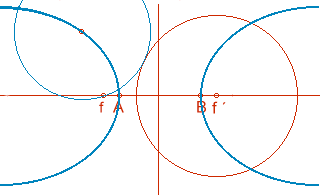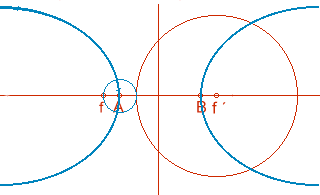
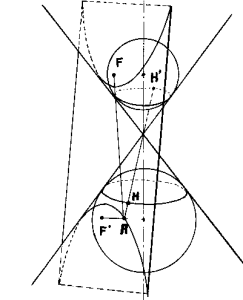
	Definición de hipérbola: lugar geométrico de puntos que son centros de circunferencias que pasan por el foco y son tangentes a la otra focal.	pulsa para ver en 3D

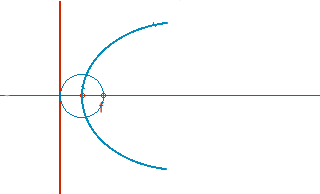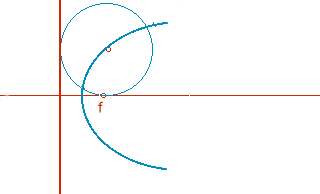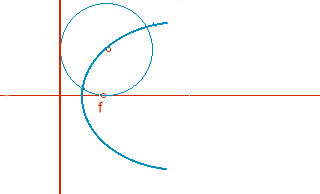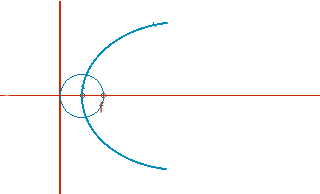
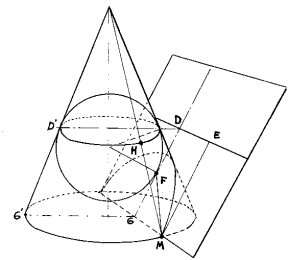
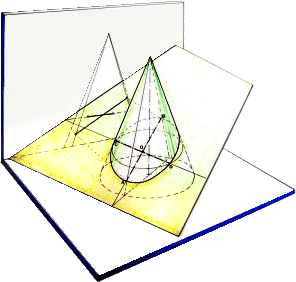
	Definición de parábola: lugar geométrico de puntos que son centros de circunferencias que pasan por el foco y son tangentes a la directriz..	pulsa para ver en 3D

		En la hipérbola observamos cómo la resta de radios vectores nos da el radio de la focal F´ (diámetro mayor), por lo que cada punto de la curva es el centro de una circunferencia tangente a la focal y de radio PF.

	Podemos obtener una sección cónica cortando una superficie cónica de revolución con un plano oblícuo. El diámetro mayor de la sección sería la recta de máxima pendiente del plano oblicuo, y el diámetro menor una horizontal de plano:	Más simple es la sección producida por un plano proyectante vertical sobre la superficie de revolución. En este caso el diámetro mayor seria una frontal del plano y el diámetro menor una recta de punta contenida en él:
	Sección por plano oblicuo	Sección por proyectante

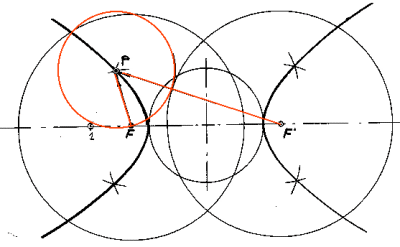
	Construcción de la parábola, elipse e hipérbola
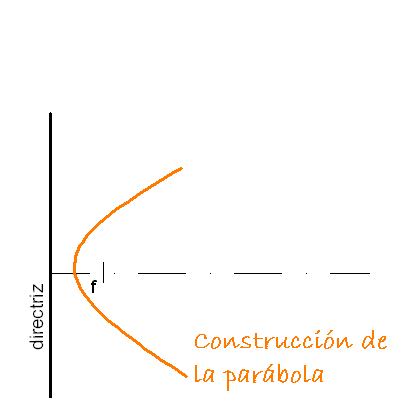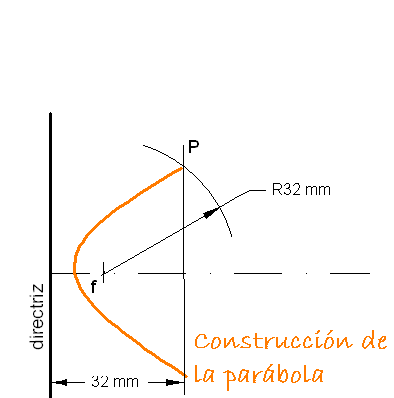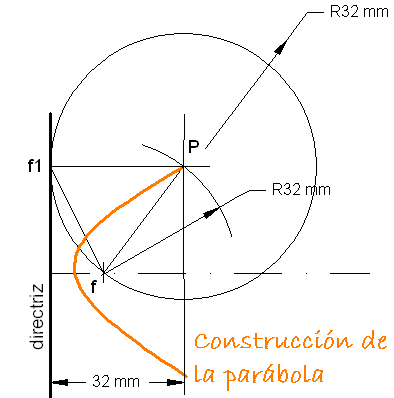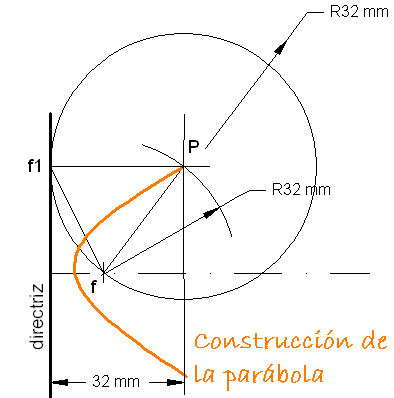
		Para hallar puntos de la parábola se utiliza el método siguiente: - Una paralela a la directríz a una distancia determinada(R) - Desde el foco y con radio R trazamos un arco que corte a la paralela. - Este punto pertenece a la parábola porque equidista del foco y la directriz. (corresponde al ejercicio de tangencias: Circunferencia que pasa por un punto y es tangente a una recta)
		Para trazar una tangente a la parábola situamos el simétrico del foco con respecto a dicha tangente en cualquier lugar de la directriz. La tangente es la mediatriz de este segmento y el punto de tangencia se obtiene trazando una perpendicular a la directriz hasta cortar a la tangente.


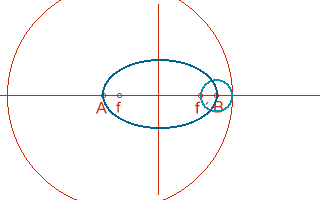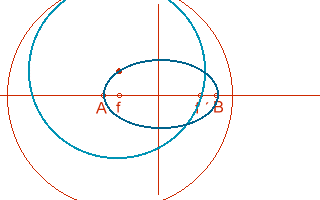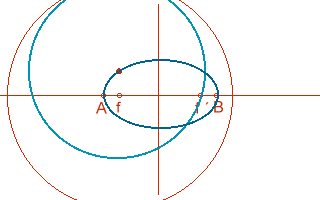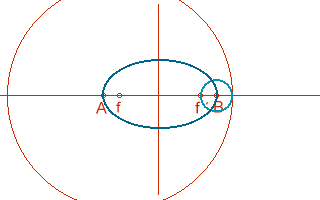
	Construcción de la elipse	Para hallar puntos de la elipse se utiliza el método siguiente: - Se divide el diámetro mayor en dos radios vectores cualesquiera. - Desde los focos y con radio igual a dichos radios vectores trazamos arcos que se corten para obtener puntos de la elipse. - Este punto pertenece a la elipse porque es el centro de una circunferencia que pasa por un foco y es tangente a la focal del otro foco. (el ejercicio consiste en: Triángulo conociendo la base (2c) y los dos lados)
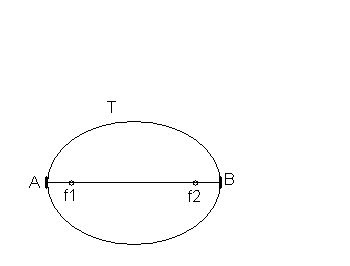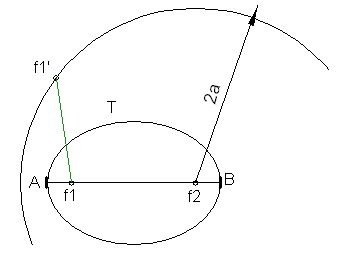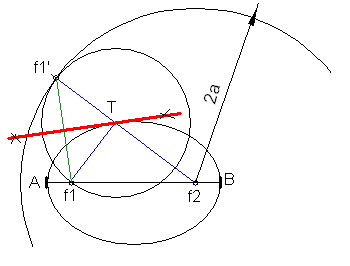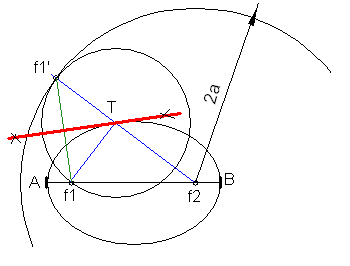
	Tangente a la elipse	Para obtener una tangente a la elipse, situamos el simétrico del foco con respecto a dicha tangente en cualquier punto de la focal del otro foco. La mediatriz del foco y su simétrico es la tangente buscada. El punto de tangencia se obtiene uniendo el simétrico con el centro de la focal.

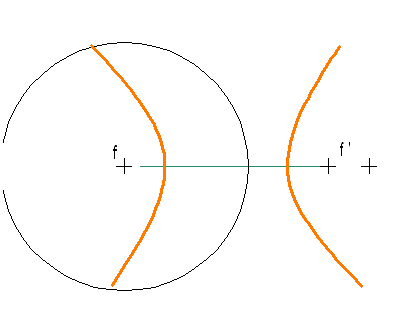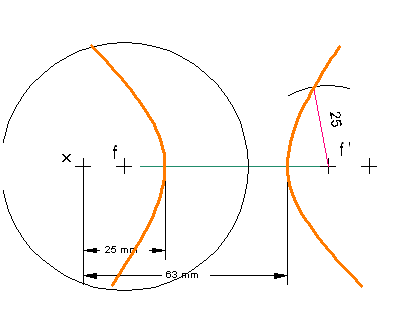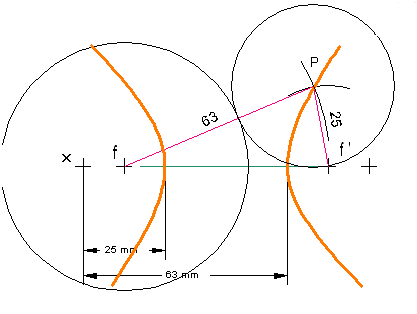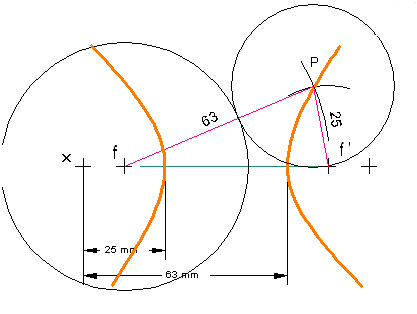
	Construcción de la hipérbola	Para hallar puntos de la hipérbola se utiliza el método siguiente: - Se marca un punto X fuera del diámetro mayor para obtener dos segmentos XA y XB(radios vectores) cuya diferencia sea 2a. - Desde los focos y con radio igual a dichos radios vectores trazamos arcos que se corten para obtener puntos de la hipérbola. - Este punto pertenece a la hipérbola porque es el centro de una circunferencia que pasa por un foco y es tangente a la focal del otro foco. (el ejercicio consiste en: Triángulo conociendo la base (2c) y los dos lados)
	Tangente a la hipérbola	Para obtener una tangente a la hipérbola, situamos el simétrico del foco con respecto a dicha tangente en cualquier punto de la focal del otro foco. La mediatriz del foco y su simétrico es la tangente buscada. El punto de tangencia se obtiene uniendo el simétrico con el centro de la focal.

		(c)T. Mendoza 2007