
 |
VICERRECTORADO DE ALUMNOS |
|---|---|
Pruebas de Acceso a la Universidad |
| MATEMATICAS I |
|---|
| CRITERIOS ESPECÍFICOS DE CORRECCIÓN |
|
MODELO DE EXAMEN 1996-97 | |||
|---|---|---|---|
| MATERIA: Matemáticas I | TIEMPO: Una hora, treinta minutos | ||
| INSTRUCCIONES:
El alumno desarrollará uno de los dos repertorios siguientes, y dará respuestas claras y concisas a cada una de las cinco cuestiones. El repertorio elegido debe figurar al principio del ejercicio. CALIFICACIÓN: La calificación máxima de cada uno de los cinco ejercicios será de 2 puntos. | |||
| REPERTORIO A | |||
| 1. Estudiar la continuidad y
derivabilidad de la siguiente función definida en la recta real por
2. Calcular la integral
3. Discutir el siguiente sistema según los valores de l , y resolverlo cuando sea posible
4. Determinar los valores de los parámetros a y b, para que las rectas
5. Se toman tres cartas de una baraja de cuarenta (cuatro palos numerados de uno al diez). Hallar la probabilidad de que salga el as de oros. | |||
| REPERTORIO B | |||
| 1. Sea
2. Estudiar para qué valores de a
las funciones
3. Determinar para qué valores del parámetro l, los siguientes sistemas tienen el mismo conjunto de soluciones:
4. Determinar un punto P de la
recta r : p :
x + y + z = -3, y s : 5. Se lanza una moneda equilibrada. Si sale cara, se sigue el juego sacando una bola de una bolsa que contiene 12 bolas numeradas del uno al doce y si sale cruz, se saca una bola de otra bolsa que contiene cuatro bolas numeradas del uno al cuatro.
| |||
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE SEPTIEMBRE DE 1.997 | ||||||
|---|---|---|---|---|---|---|
| MATERIA: Matemáticas I (Obligatoria) | TIEMPO: Una hora, treinta minutos | |||||
INSTRUCCIONES:
CALIFICACIÓN:
| ||||||
| REPERTORIO A | ||||||
1. Comprobar que
A2 = 2A - I
siendo
Determinar la matriz inversa de A y la matriz A8. 2. Calcular las ecuaciones de la recta que pasa por el punto de intersección de las rectas:
3. Calcular:
4. Encontrar un
número a > 1 para que el área limitada por la curva
5. La urna A contiene cuatro bolas blancas y dos negras y en la urna B hay dos bolas blancas y cinco negras. Se toma al azar una bola de A y, sin mirarla, se introduce en B. A continuación se extraen sin reemplazamiento dos bolas de B. Hallar la probabilidad de que ambas sean blancas. | ||||||
| REPERTORIO B | ||||||
1. Probar
que las rectas 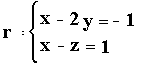 y y 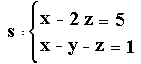 son
paralelas. Determinar la ecuación del plano p que las contiene. son
paralelas. Determinar la ecuación del plano p que las contiene.
2. Discutir según los valores de l el sistema de ecuaciones
3. Demostrar que la
función 4.
Encontrar el volumen de la figura que se obtiene girando la
gráfica de la función 5. Tenemos un dado cargado en el que los números pares tienen doble probabilidad de salir que los impares. Calcular la probabilidad de que, al lanzarlo, la puntuación obtenida sea mayor o igual que cuatro. | ||||||
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE SEPTIEMBRE DE 1.997 | |||
|---|---|---|---|
| MATERIA: Matemáticas I (Optativa) | TIEMPO: Una hora, treinta minutos | ||
INSTRUCCIONES:
CALIFICACIÓN:
| |||
| REPERTORIO A | |||
| 1. Discutir el sistema
2. Determinar, en función del parámetro l , la posición relativa de las rectas: 3. Calcular el valor de la integral definida
4. Estudiar la
continuidad y derivabilidad de la siguiente función definida en la recta
real por 5. Una persona tiene un despertador que suena con probabilidad 0,9. Si suena, se despertará con probabilidad 0,7 y llegará puntual al trabajo. Si no suena, se despertará a tiempo para llegar puntual al trabajo con probabilidad 0,3.
| |||
| REPERTORIO B | |||
| 1. Dado el
siguiente conjunto de planos, estudiar su posición relativa según el valor
de a:
2. Determinar el
valor del parámetro l
para el que existe una recta s que pasa por el punto P = (1 +
l , 1 – l ,
l ), corta a la recta 3. Se considera la función
Calcular su máximo, justificando la respuesta. 4. Se toman cuatro cartas de una baraja de cuarenta (cuatro palos numerados del uno al diez). Hallar la probabilidad de que sean de números distintos. 5. Calcular el límite
| |||
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE JUNIO DE 1.997 | ||||
|---|---|---|---|---|
| MATERIA: Matemáticas I (Obligatoria) | TIEMPO: Una hora, treinta minutos | |||
INSTRUCCIONES:
CALIFICACIÓN:
| ||||
| REPERTORIO A | ||||
1. Dada la
matriz A =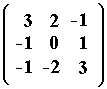 determinar
todas las matrices no nulas determinar
todas las matrices no nulas2. Calcular el valor del parámetro a para que las rectas
3. Representar la gráfica de la siguiente función:
estudiando máximos, mínimos, asíntotas, puntos de inflexión, concavidad y convexidad. 4. Sea
Calcular F’(x). 5. Se toman sin reemplazamiento tres cartas de una baraja de cuarenta (cuatro palos numerados del uno al diez). Hallar la probabilidad de que salga el as de oros. | ||||
| REPERTORIO B | ||||
1. Determinar todas las matrices A= 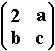 tales que su inversa sea 2I- A, donde I
=
tales que su inversa sea 2I- A, donde I
=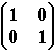
2. Hallar el punto de
la recta x = -2y = -2z cuya distancia al origen es el
doble que su distancia a la recta 3. Sea f una función continua y derivable tal que f(0) = 3. Calcular cuánto tiene que valer f(5) para asegurar que en [0,5] existe una c tal que f’(c) = 8. 4. Calcular la
integral 5. Sabiendo que
P(a) = 0,4, P(B) = 0,5 y P (A
donde Ac representa el suceso contrario (o complementario) de A. | ||||
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE JUNIO DE 1.997 | |||
|---|---|---|---|
| MATERIA: Matemáticas I (Optativa) | TIEMPO: Una hora, treinta minutos | ||
INSTRUCCIONES:
CALIFICACIÓN:
| |||
| REPERTORIO A | |||
| 1. Discutir la compatibilidad del siguiente sistema según los valores
del parámetro a:
2. Dadas las rectas determinar las ecuaciones de la recta s que corta a r y a r’ y es paralela a r’’ : x = y = z. 3. Calcular la integral
4. Dada la función p(x) = ax3 + bx2 + cx + d, determinar el valor o valores de los parámetros a, b, c y d para que dicha función tenga un mínimo relativo en (0,1) y un máximo relativo en x = 2 y probar que todas tienen un punto de inflexión con la misma abscisa. 5. Se toman sin reemplazamiento tres cartas de una baraja de 40 (cuatro palos numerados del 1 al 10). Hallar la probabilidad de que las cartas extraídas sean de tres palos distintos. | |||
| REPERTORIO B | |||
| 1.Calcular
los valores del parámetro l para que la inversa de la matriz
coincida con su opuesta 2. Determinar los
puntos de la recta r: 3. Calcular los siguientes límites:
4. Sea f(x) = 3 + x5(x - 3)4. Probar que la función derivada f’(x) posee al menos una raíz en el intervalo abierto (0,3). 5. Un opositor se presenta a un ejercicio oral en el que, para superarlo, debe contestar correctamente al menos a dos de los tres temas que se le proponen. Cada tema propuesto se extra al azar. El primero de un grupo de 40, el segundo de uno de 50 y el tercero de uno de 60. Sabiendo que un opositor que ha superado la prueba no preparó 10 temas de cada grupo, ¿cuál es la probabilidad de que haya contestado un tema del primer grupo?. | |||
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE JUNIO DE 1.996 | |
|---|---|
| MATERIA: Matemáticas I (Obligatoria) | TIEMPO: Una hora, treinta minutos |
INSTRUCCIONES:
CALIFICACIÓN:
| |
| REPERTORIO A | |
| 1.
Calcular el valor de la integral
2. Hallar a y
b para que la función 3. Hallar una matriz dos por dos, distinta de I y de -I, cuya inversa coincida con su traspuesta, siendo I la matriz
4. Hallar los puntos cuya distancia al origen es el triple que su distancia a la recta
5. Se lanza tres veces un dado equilibrado de seis caras numeradas del uno al seis. Hallar la probabilidad de que la suma de los resultados sea igual a ocho. | |
| REPERTORIO B | |
| 1. Sea
2. Dada la función
y = ax4 + 3bx3 -
3x2 - ax, calcular los valores de
a y b sabiendo que la función presenta
dos puntos de inflexión, uno en x = 1 y otro en 3. Resolver el sistema
4. Calcular la
ecuación del plano que pasa por el punto (1, 0, -1), es paralelo a
la recta 5. Las siete bolas blancas y las cinco negras de una urna tienen la misma probabilidad de ser extraídas. Se extraen sucesivamente y sin reemplazamiento dos bolas. Hallar la probabilidad de que sean del mismo color. | |
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE JUNIO DE 1.996 | ||||
|---|---|---|---|---|
| MATERIA: Matemáticas I (Optativa) | TIEMPO: Una hora, treinta minutos | |||
INSTRUCCIONES:
CALIFICACIÓN:
| ||||
| REPERTORIO A | ||||
| 1. Hallar
la derivada enésima de 2. Aplicar el teorema
del Valor Medio a la función f(x) = Ln x en el intervalo [1,
e2] determinando el valor 3. Discutir y resolver, según los valores de l
4. Dadas las rectas
5. Se tiene un dado de seis caras cargado en el que la probabilidad de que salga un número es inversamente proporcional al número. Calcular la probabilidad de que al lanzar el dado salga un múltiplo de 2. | ||||
| REPERTORIO B | ||||
| 1. Sea
2. Descomponer el número 100 en dos sumandos tales que el doble del cuadrado del primero más tres veces el cuadrado del segundo sea mínimo. 3. Se sabe (no es necesario que lo compruebe) que la matriz
4. Dados los planos p: mx + y + z = 1 p‘: x + my + z = 1 p": x + y + mz = 1
5. En una urna con 3 bolas blancas y 4 bolas negras se extraen, con reemplazamiento, 4 bolas. Hallar la probabilidad de que ninguna sea blanca. | ||||
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE SEPTIEMBRE DE 1.996 | |||
|---|---|---|---|
| MATERIA: Matemáticas I (Obligatoria) | TIEMPO: Una hora, treinta minutos | ||
| INSTRUCCIONES:
El alumno desarrollará uno de los dos repertorios siguientes, y dará respuestas claras y concisas a cada una de las cinco cuestiones. El repertorio elegido debe figurar al principio del ejercicio. CALIFICACIÓN: La calificación máxima de cada uno de los cinco ejercicios será de 2 puntos. | |||
| REPERTORIO A | |||
| 1. Estudiar la continuidad y derivabilidad de la siguiente función
definida en la recta real por
2. Calcular la integral
3. Discutir el siguiente sistema según los valores de l , y resolverlo cuando sea posible
4. Determinar los valores de los parámetros a y b, para que las rectas
5. Se toman tres cartas de una baraja de cuarenta (cuatro palos numerados de uno al diez). Hallar la probabilidad de que salga el as de oros. | |||
| REPERTORIO B | |||
| 1. Sea
2. Estudiar para qué
valores de a las funciones
3. Determinar para qué valores del parámetro l, los siguientes sistemas tienen el mismo conjunto de soluciones:
4. Determinar un
punto P de la recta r : p :
x + y + z = -3, y s : 5. Se lanza una moneda equilibrada. Si sale cara, se sigue el juego sacando una bola de una bolsa que contiene 12 bolas numeradas del uno al doce y si sale cruz, se saca una bola de otra bolsa que contiene cuatro bolas numeradas del uno al cuatro.
| |||
EJERCICIO PROPUESTO EN LA CONVOCATORIA DE SEPTIEMBRE DE 1.996 | |||
|---|---|---|---|
| MATERIA: Matemáticas I (Optativa) | TIEMPO: Una hora, treinta minutos | ||
| INSTRUCCIONES:
El alumno desarrollará uno de los dos repertorios siguientes, y dará respuestas claras y concisas a cada una de las cinco cuestiones. El repertorio elegido debe figurar al principio del ejercicio. CALIFICACIÓN: La calificación máxima de cada uno de los cinco ejercicios será de 2 puntos. | |||
| REPERTORIO A | |||
| 1. ¿Se
verifican las hipótesis del Teorema de Rolle para la función
ƒ(x) = |2x–3| – 7, -2 2. Determinar el volumen generado al girar respecto al eje OX (eje de abscisas) la región acotada por las gráficas de las funciones ƒ(x) = x2 y g(x) = 2x. 3. Sea A la
matriz 4. Hallar la distancia entre las rectas r y s, siendo: 5. La urna A contiene tres bolas blancas y dos negras y en la urna B hay dos bolas blancas y cinco negras. Se toma al azar una bola de A y se introduce, sin mirarla, en B. A continuación se extraen sin reemplazamiento dos bolas de B. Hallar la probabilidad de que ambas sean blancas. | |||
| REPERTORIO B | |||
| 1. Se
divide una cuerda de longitud 1 en dos partes, no necesariamente iguales,
para construir un cuadrado y una circunferencia. Probar que de todas las
posibilidades, la que encierra un área total mínima surge cuando el radio
del círculo es la mitad que el lado del cuadrado.
2. Dibujar la gráfica de la función
3. Indicar para qué valores de a tiene solución única el sistema:
4. Hallar la intersección de la recta r, determinada por los puntos A = (1,6,3) y B = (2,6,0) con el plano: p : x - y + 3z = 2. 5. Se toman dos cartas de una baraja de cuarenta (cuatro palos numerados del uno al diez). Calcular la probabilidad de que las dos sean del mismo número o del mismo palo. | |||
© Universidad Complutense de Madrid, 1997